December 31 2022
How to Solve Any Sudoku Puzzle in One Second
by Brian Dunagan

Unsplash - @iamfrancismorgan

My friend pointed out an excellent article by Peter Norvig titled Solving Every Sudoku Puzzle. Norvig is an Education Fellow at Stanford Institute for Human-Centered AI, co-authored “Artificial Intelligence: A Modern Approach”, the most popular AI textbook, and served as a director of research and search quality at Google.

This is Sudoku: fill in every blank square with a number between 1 and 9 such that every row, every column, and every 3x3 group has every digit.

Example Sudoku Puzzle

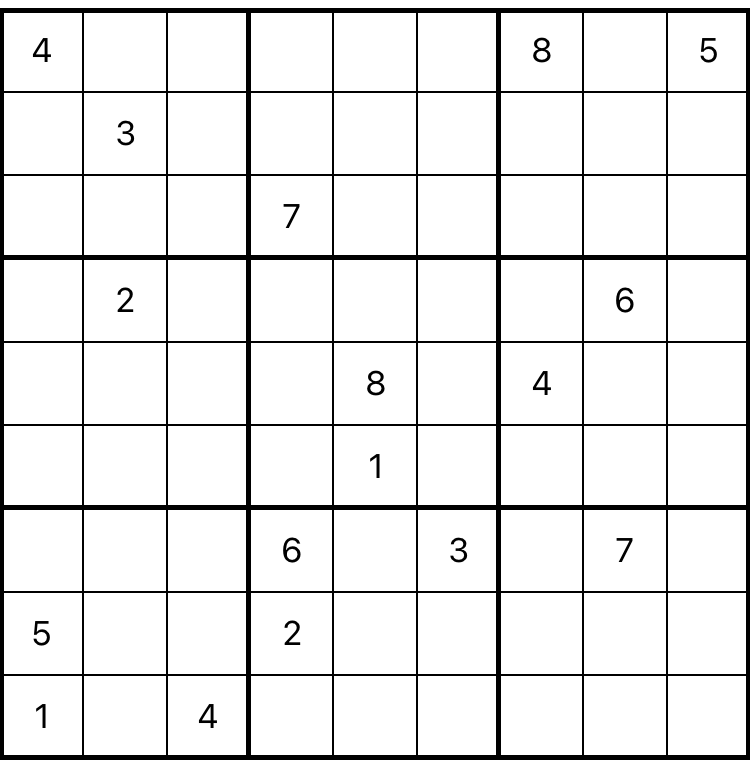
I was a complete novice to Sudoku when I started this project. I had casually played it before, but my naive mental algorithm was a mix of constraint propagation and search, without any systematic method to it. In his article, Norvig walked through how to use constraint propagation and backtracking search to quickly solve any valid Sudoku puzzle. His Python version was able to do so in one second for the world’s hardest puzzles.

I skimmed Norvig’s general approach (summarized below) and then attempted to fill in the details myself with a Ruby implementation. The process took a couple iterations and pushed me to understand the problem space far better than I would have simply reading the article and Norvig’s Python implementation.

Let’s walk through the different challenges.

Problem Space

Sudoku has 10^21 potential solutions, and the minimum number of supplied values is 17. A researcher actually spent a year proving that no 16-value Sudoku puzzles existed, according to MIT Tech Review. Fittingly, Norvig’s example puzzle (pictured above) has 17 values.

Each square in the 9x9 grid can have a value between 1 and 9. These squares are grouped into “units”: columns, rows, and 3x3 groups. Each unit has nine squares (peers), so each unit has one of every digit. If a unit already has a value assigned, like “4” in the first square (A1 in Sudoku parlance), then no other square can contain that value. By converting the grid that we see into representation of known and potential values (A1->4, A2->12356789...), we can evaluate each unit according to a set of constraints.

Constraint Propagation

There are two constraints that we can use to reduce the space of possibilities:

Elimination: If a square has only one value, eliminate that value from all other peers.
Assignment: If a square is the only peer with a certain value, that value must belong to that square.

For every elimination, we can attempt an assignment, and for every assignment, we can attempt further eliminations, recursively narrowing the potential value space for the puzzle.

In practice, easy and medium difficulty Sudoku puzzles can be solved without search by simply running eliminations and assignments recursively.

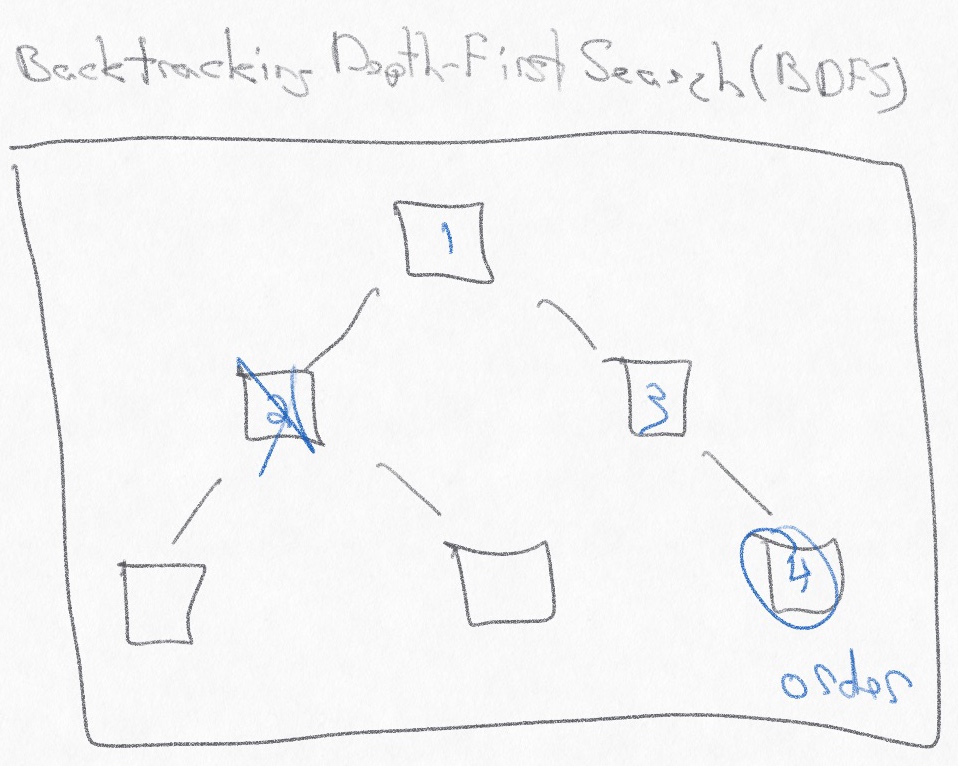
Search

Constraint propagation only gets us so far. After we’ve limited the potential values using eliminations and assignments, we need to search the problem space: choose a possible value for a square and see if it’s correct. A backtracking search leverages constraints to prune a given branch and backtrack as soon as the remaining possibilities on that branch are not valid. I used a backtracking depth-first search in my implementation.

Backtracking Depth-First Search (BDFS)

Implementations Details

Norvig wrote his implementation in Python. I wrote mine in Ruby. They’re both great, high-level languages, but they have important differences that only manifested when I tested difficult puzzles.

In particular, Python has lazy evaluation of generator functions. In some(), the expression e is not evaluated until it’s needed, so the first time it succeeds, it returns and does not evaluate the rest.

def some(seq):
    "Return some element of seq that is true."
    for e in seq:
        if e: return e
    return False

Ruby does not have lazy evaluation, so the function needs to check an instance variable instead to break out of the search.

Norvig picked an excellent puzzle as the example because there are only 17 initial numbers, compared to 36 in easy puzzles and 22 in hard ones. Moreover, the puzzle seems designed to trip up naive search algorithms. My early iterations failed on his example because squares with the smallest number of potential values needed the larger number assigned, and my code guessed the lowest one and could never recover after that. It was a great example that ensured I didn’t prematurely stop improving the algorithm.

However, only testing with one puzzle is not a good QA practice, so I built out a test framework with 60 puzzles of varying difficulty to ensure my implementation worked on a variety of puzzles beyond Norvig’s example. To ease debugging, I added two functions for displaying the current state of the puzzle grid in Terminal: one for the actual values and one for the potential values. The visual aid helped debug issues with the search algorithm.

def self.format_grid(grid)
    # Print grid as numbers and dots.
    grid.chars.each_slice(9).to_a.each_with_index do |row, i|
        log (row.slice(0,3).join + "|" + row.slice(3,3).join + "|" + row.slice(6,3).join).split("").join(" ")
        log "------+------+------" if i % 3 == 2 && i < 8
    end
end

Sudoku Grid in Terminal

def display_values(values)
    values.values.each_slice(9).to_a.each_with_index do |row, i|
        log row[0..2].collect {|r| r.center(9)}.join(" ") + "|" + row[3..5].collect {|r| r.center(9)}.join(" ") + "|" + row[6..8].collect {|r| r.center(9)}.join(" ")
        log "-----------------------------+-----------------------------+-----------------------------" if i % 3 == 2 && i < 8
    end
    log ""
end

Sudoku Potential Values in Terminal

After I finished debugging my version, I ported Norvig’s Python implementation into Ruby to see how they compared. Norvig’s algorithm was vastly faster than mine was: from 3x faster (0.004 seconds vs 0.01 seconds) for easy puzzles to 178x faster for the hardest puzzle available (Unsolvable #28): 0.2 seconds vs 34 seconds.

The implementations were close for puzzles that only required constraint propagation, but mine was much slower at search for two reasons:

Overzealous Constraint Propagation: My version wasted a tremendous amount of time performing constraint propagation on every square during every search, rather than focusing on the square being tested and its affected peers in each unit.
Wasted Data Conversions: My version passed each grid to be tested as a string to the next search, forcing each run to recreate the potential values of each square in the grid rather than leaving the internal representation as a set of known/potential values for each square.

I preserved my Ruby approach along with my Ruby port of the Python version in a GitHub repo for comparison along with the sudoku.csv test framework and results: bdunagan/SudokuAI.

SudokuAI